Page 37 - 白楊17.FIT)

揖設(shè)計意圖銥引導(dǎo)學(xué)生發(fā)現(xiàn)從特殊到一般的研究 殊點和單調(diào)性遙 在這個過程中袁有意識地向?qū)W生滲透

x 1 x 數(shù)形結(jié)合的思想方法袁引導(dǎo)學(xué)生野以形助數(shù)冶遙
方法袁在研究了y=2 和y=( ) 這一對函數(shù)之后袁再研
2
究具有類似對稱關(guān)系的其他幾對函數(shù)袁 概括它們的
共同特征遙 通過選取底數(shù)a淵a躍0袁且屹1冤的若干個不
同的值袁 在同一直角坐標(biāo)系內(nèi)畫出相應(yīng)的指數(shù)函數(shù)

的圖像遙 觀察這些圖像的位置堯公共點和變化趨勢袁
x
尋找它們的共性袁概括出指數(shù)函數(shù)y=a 淵a躍0袁且屹1冤
的性質(zhì)遙
教師將以上函數(shù)的圖像放置于同一直角坐標(biāo)系
內(nèi)袁 引導(dǎo)學(xué)生觀察函數(shù)的圖像袁 歸納指數(shù)函數(shù)的性
質(zhì)袁尋找共性遙
淵1冤這些函數(shù)的圖像都過點(0,1)曰淵2冤函數(shù)的定
義域都是(-肄,肄)袁值域都是(0,+肄)曰淵3冤當(dāng)0約a約1時袁函 深
淵三冤典例剖析 度
數(shù)圖像均呈下降趨勢袁即函數(shù)為減函數(shù)曰當(dāng)a躍1時袁函 教
例1院說出下列各題中兩個值的大小院
數(shù)圖像均呈上升趨勢袁即函數(shù)為增函數(shù)遙 研
.5
-2
-1
3
淵1冤1.72 __1.7 曰淵2冤0.8 __0.8 曰 窯
問題3院這幾個函數(shù)的圖像是否能代表一般的指 新
0.5
淵3冤1.7 __ 0.8 2.5 教
數(shù)函數(shù)的圖像鑰 我們得到的性質(zhì)是否推廣到一般的
咱規(guī)律方法暫比較冪的大小的方法 材
指數(shù)函數(shù)的性質(zhì)鑰 研
淤同底數(shù)冪比較大小時構(gòu)造指數(shù)函數(shù)袁 根據(jù)其
利用信息技術(shù)演示a取任意值時的大量圖像袁這 究
單調(diào)性比較曰 于指數(shù)相同底數(shù)不同時分別畫出以兩 35
樣探究的好處是底數(shù)a的取值自然袁所作函數(shù)的圖像
冪底數(shù)為底數(shù)的指數(shù)函數(shù)圖像袁當(dāng)x取相同冪指數(shù)時
也是自然產(chǎn)生的袁為下一步歸納性質(zhì)作好鋪墊遙
可觀察出函數(shù)值的大小曰盂底數(shù)堯指數(shù)都不相同時袁
揖設(shè)計意圖銥畫出幾個特殊函數(shù)的圖像袁觀察這
取與其中一底數(shù)相同與另一指數(shù)相同的冪與兩數(shù)比
幾個函數(shù)的圖像來討論函數(shù)的性質(zhì)援這會帶來一系列
較袁或借助野1冶與兩數(shù)比較曰榆當(dāng)?shù)讛?shù)含參數(shù)時袁要按
問題院 為什么這幾個函數(shù)的圖像就可以代表一般的
底數(shù)a>1和0<a<1兩種情況分類討論遙
指數(shù)函數(shù)的圖像鑰由此得到的性質(zhì)是否可靠鑰為什么
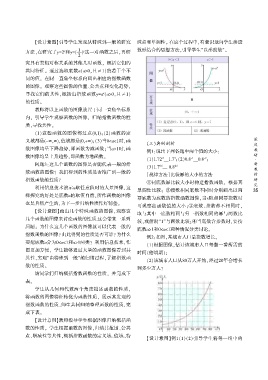
例2院如圖袁某城市人口呈指數(shù)增長遙
要把底數(shù)a分為0約a約1和a躍1兩類鑰 利用信息技術(shù)袁作
淵員冤根據(jù)圖像袁估計該城市人口每翻一番所需的
圖更加方便袁 學(xué)生能夠通過大量的函數(shù)圖像看到其
時間淵倍增期冤曰
共性袁實現(xiàn)野由特殊到一般冶的歸納過程袁了解指數(shù)函
淵圓冤該城市人口從80萬人開始袁經(jīng)過20年會增長
數(shù)的性質(zhì)遙
到多少萬人鑰
請同學(xué)們歸納概括指數(shù)函數(shù)的性質(zhì)袁 并完成下
表遙
學(xué)生從幾何和代數(shù)兩個角度描述函數(shù)的性質(zhì)袁
將函數(shù)的圖像特征轉(zhuǎn)化為函數(shù)性質(zhì)袁 展示其發(fā)現(xiàn)的
指數(shù)函數(shù)的性質(zhì)袁師生共同歸納整理函數(shù)的性質(zhì)袁完
成下表遙
揖設(shè)計意圖銥教師指導(dǎo)學(xué)生根據(jù)圖像歸納概括函
數(shù)的性質(zhì)遙 學(xué)生根據(jù)函數(shù)的圖像袁歸納其范圍堯公共
點堯增減性等共性袁概括指數(shù)函數(shù)的定義域堯值域堯特
揖設(shè)計意圖銥例1淵1冤淵2冤引導(dǎo)學(xué)生將每一組中的